

Furthermore, G G G is the symmedian point of △ A ′ B ′ C ′ \triangle A'B'C' △ A ′ B ′ C ′.įinally, the medians of △ A ′ B ′ C ′ \triangle A'B'C' △ A ′ B ′ C ′ pass through the midpoints of A B, B C, AB, BC, A B, B C, and C A CA C A, so the medians of △ A ′ B ′ C ′ \triangle A'B'C' △ A ′ B ′ C ′ and △ A B C \triangle ABC △ A B C intersect at the midpoints of the original triangle. The class has a Fill, Stroke, and other rendering properties that Geometry and its derived classes lack. O O O is the centroid of triangle A ′ B ′ C ′ A'B'C' A ′ B ′ C ′. If A ′, B ′, C ′ A', B', C' A ′, B ′, C ′ are the circumcenters of triangles B C G, A C G, A B G, BCG, ACG, ABG, B C G, A C G, A B G, respectively, then There are some basic facts about the medians. Where H H H is the orthocenter of the triangle. A median of a triangle is a line segment that joins the vertex of a triangle to the midpoint of the opposite side. ( 1 ) PA^2+PB^2+PC^2+2(PD^2+PE^2+PF^2)=3\left(3PG^2+\dfracOH, G H = 3 2 O H, G O = 3 1 O H , In normal median, we find a point that has minimum sum of distances.
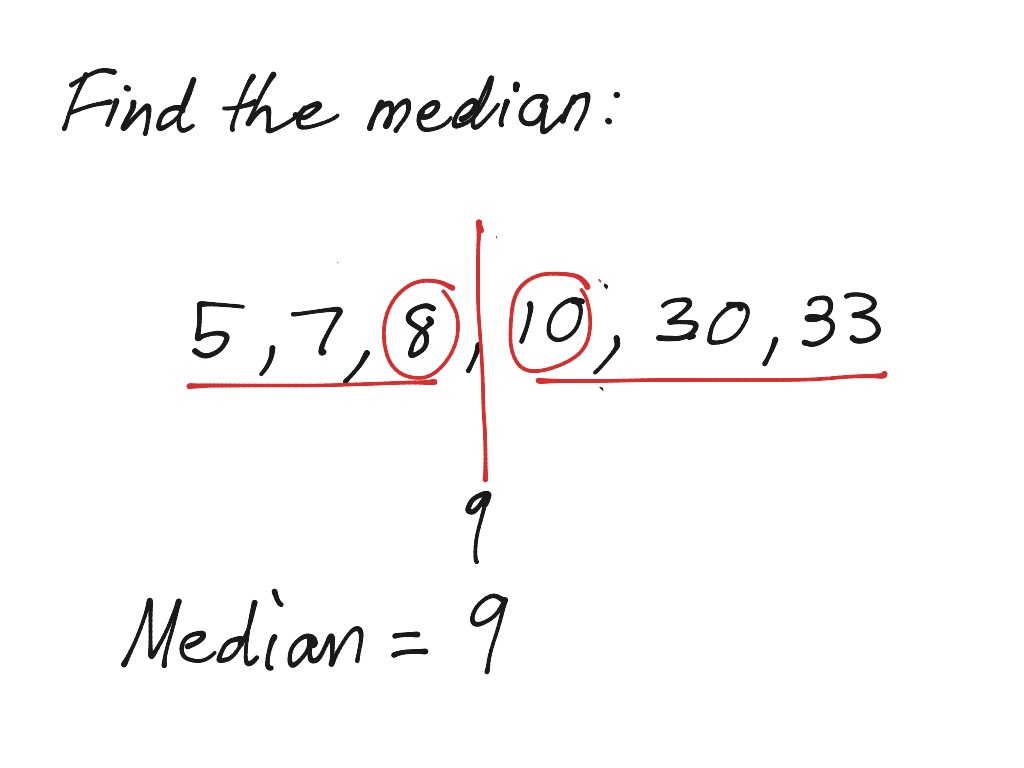
P A 2 + P B 2 + P C 2 + 2 ( P D 2 + P E 2 + P F 2 ) = 3 ( 3 P G 2 + G A 2 + G B 2 + G C 2 2 ). This can be done by first constructing a perpendicular bisector. Use the formula on △ A D P, △ B E P, △ C F P \triangle ADP,~\triangle BEP,~\triangle CFP △ A D P, △ B E P, △ C F P and add them together: A median of a triangle is a line segment from a vertex to the midpoint of the opposite side.

Let D D D be the point where A G AG A G and B C BC B C meet, E E E the point where B G BG B G and C A CA C A meet, and F F F the point where C G CG C G and A B AB A B meet. This is a consequence of the more general property that A B 2 + B C 2 + C A 2 = 3 ( G A 2 + G B 2 + G C 2 ). AB^2+BC^2+CA^2=3\big(GA^2+GB^2+GC^2\big). Go through the example given below to understand the method of finding the median in this case. We can also say, a median from any vertex bisects. The centroid divides each median into two parts, which are always in the ratio 2:1.Ī B 2 + B C 2 + C A 2 = 3 ( G A 2 + G B 2 + G C 2 ). A median of a triangle is a line segment from the vertex to the mid-point of the side opposite to that vertex. The three medians also divide the triangle into six triangles, each of which have the same area. The squared median drawn to a side of a triangle is equal to one half of the sum of the squares of the lengths of the two other sides minus the squared. The centroid of the triangle separates the median in the ratio of 2: 1. The median of a triangle can be constructed by drawing a line segment from the vertex of the triangle to the midpoint of the opposite side. Every triangle has exactly three medians, one from each vertex, and they all intersect each other at the triangles centroid.In the case of isosceles and equilateral triangles, a median bisects any angle at a vertex whose two adjacent sides are equal in length. He has a masters degree in writing and literature.

In the case of isosceles and equilateral triangles, a median bisects any angle at a. In geometry, a median of a triangle is a line segment joining a vertex to the midpoint of the opposing side. Every triangle has exactly three medians, one from each vertex, and they all intersect each other at the triangle's centroid. The median is a line that joins the midpoint of a side and the opposite vertex of the triangle. In geometry, a median of a triangle is a line segment joining a vertex to the midpoint of the opposite side, thus bisecting that side. It is also defined as the point of intersection of all the three medians. The three medians meet at one point called centroid - point G. The point in which the three medians of the triangle intersect is known as the centroid of a triangle. The centroid is the intersection of the three medians. In a triangle, a median is a line joining a vertex with the mid-point of the opposite side. Each median divides the triangle into two triangles of equal area.
#MEDIAN GEOMETRY FREE#
If you have any doubts, queries or suggestions regarding this article, feel free to ask us in the comment section and we will be more than happy to assist you.A median of a triangle is the line segment between a vertex of the triangle and the midpoint of the opposite side. We hope this detailed article on medians of a triangle helped you in your studies. The centroid of a triangle is the intersection of the three medians, or the average of the three vertices. So, \(D\) and \(E\) are midpoints on \(PQ\) and \(PR\), respectively. In the first figure above, \(QE\) and \(DR\) are median on \(PR\) and \(PQ\) respectively.


 0 kommentar(er)
0 kommentar(er)
